Transition Matrix Method
for Polymers Confined to a Lattice, Part 1
Polymers can assume a huge number of states (conformations) which makes the calculation of their thermodynamical properties extremely difficult. To
simplify the problem, the number of available
states has to be reduced, which is often done by assuming discrete states. One of the most popular models is the
quasi-crystalline lattice model where groups of atoms
are treated as single interaction units which are restricted to a lattice.1,2 As has been shown
by many authors, lattice problems may be best solved using a transition matrix formalism.3-8
The matrix method is very convenient and can be
adapted to solve many lattice walk problems. One of the oldest models that utilizes this formalism was developed by DiMarzio and Rubin
(1971) to describe the behavior of polymer lattice chains
in confined space.3-5
2D Lattice Polymer Chain
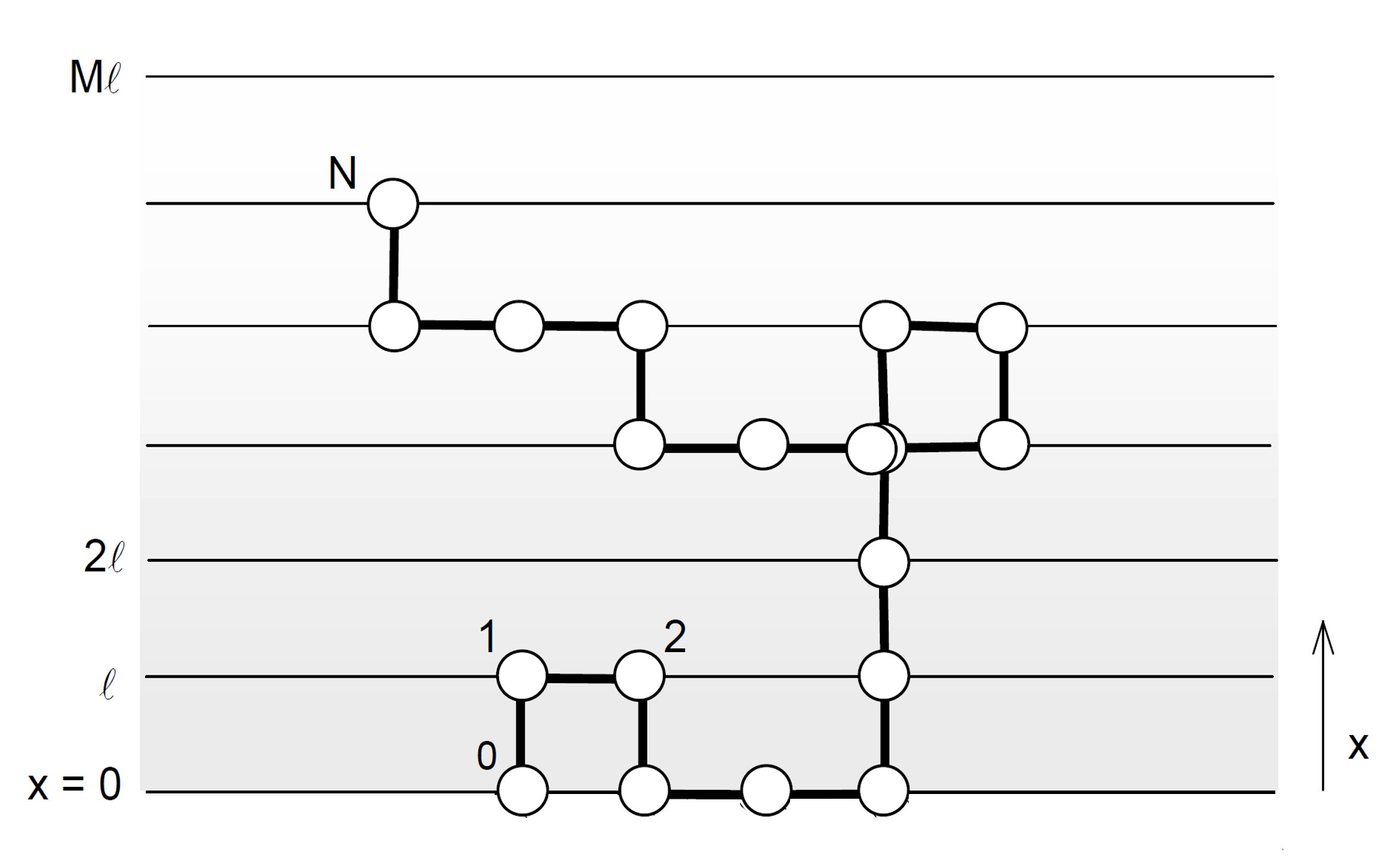
2D Lattice Polymer Chain
Let us consider a lattice chain near an impermeable interface. The lattice can be considered as an array of layers numbered i = 1, 2, ..., M with sites similar to the surface layer (see figure above). The interface corresponds to the y - z lattice plane through the point x = 0. Successive lattice planes through x = l, 2l, 3l.. represent the solution phase where l is the lattice constant. Each site is surrounded by z nearest-neighbor sites. λ0 z sites are located in the same layer and λ1 z = z (1 - λ0) / 2 in one of the adjacent layers. Far from the surface plane, all random walk configurations of a given length are equally likely. However walks of the same length that touch the interface will have different probabilities, depending on the interaction energy εpw between the chain segments and the interface.
Consider a chain of N + 1 repeat units that has its first unit in the surface layer, i = 0. This situation is equivalent to a N-step restricted random walk that starts in the surface layer. Obviously, after N steps, the random walker can be located in any one of the layers from x = 0 to x = N. Therefore, at the Nth step N + 1 probabilities have to be considered: G(N, 0), G(N, 1l)...G(N, Nl), where G(N, kl) is the unnormalized probability that a walk ends in the kth lattice layer at the Nth step. If the last segment is in layer k ≥ 1, then the last but one has to be in layer k - 1, k or k + 1. The recurrence relation for this problem is evidently
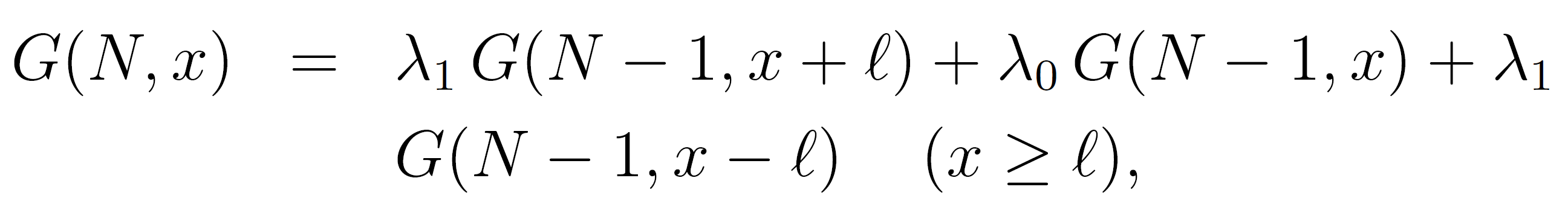
and for the segments at the interface:
![]()
where χs = εpw / kT is a dimensionless adsorption energy parameter first introduced by Silberberg.10 The N + 1 recurrence relations can be written in matrix form as
![]()
where G(N) is the column vector of all end segment probabilities G(N,i):
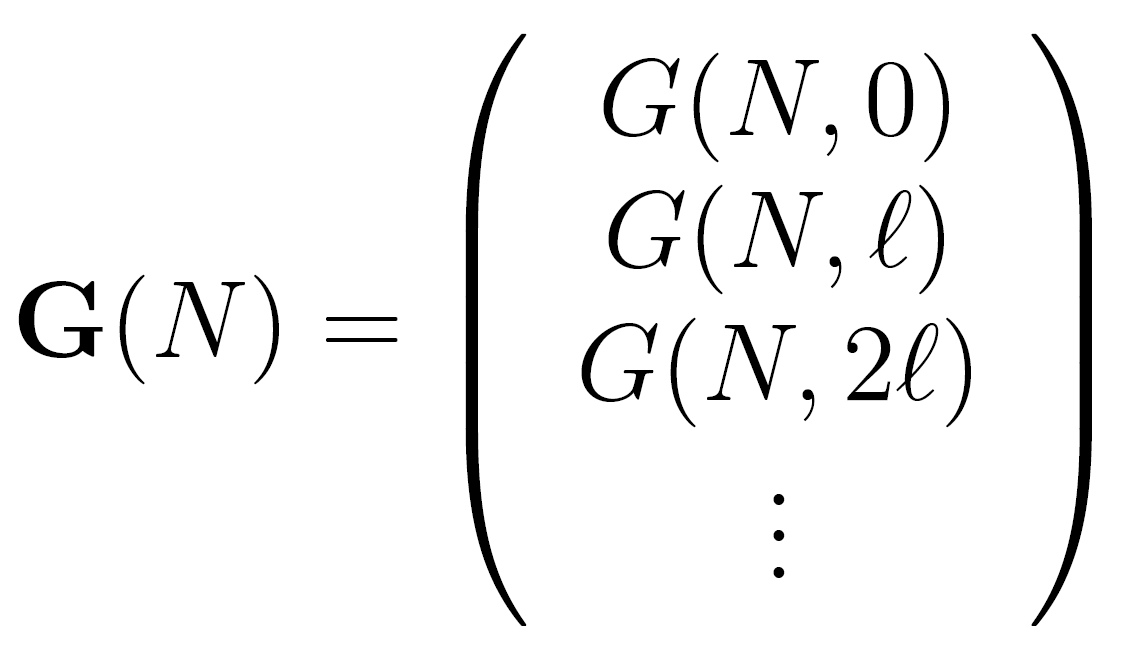
The transition probability matrix W is given by
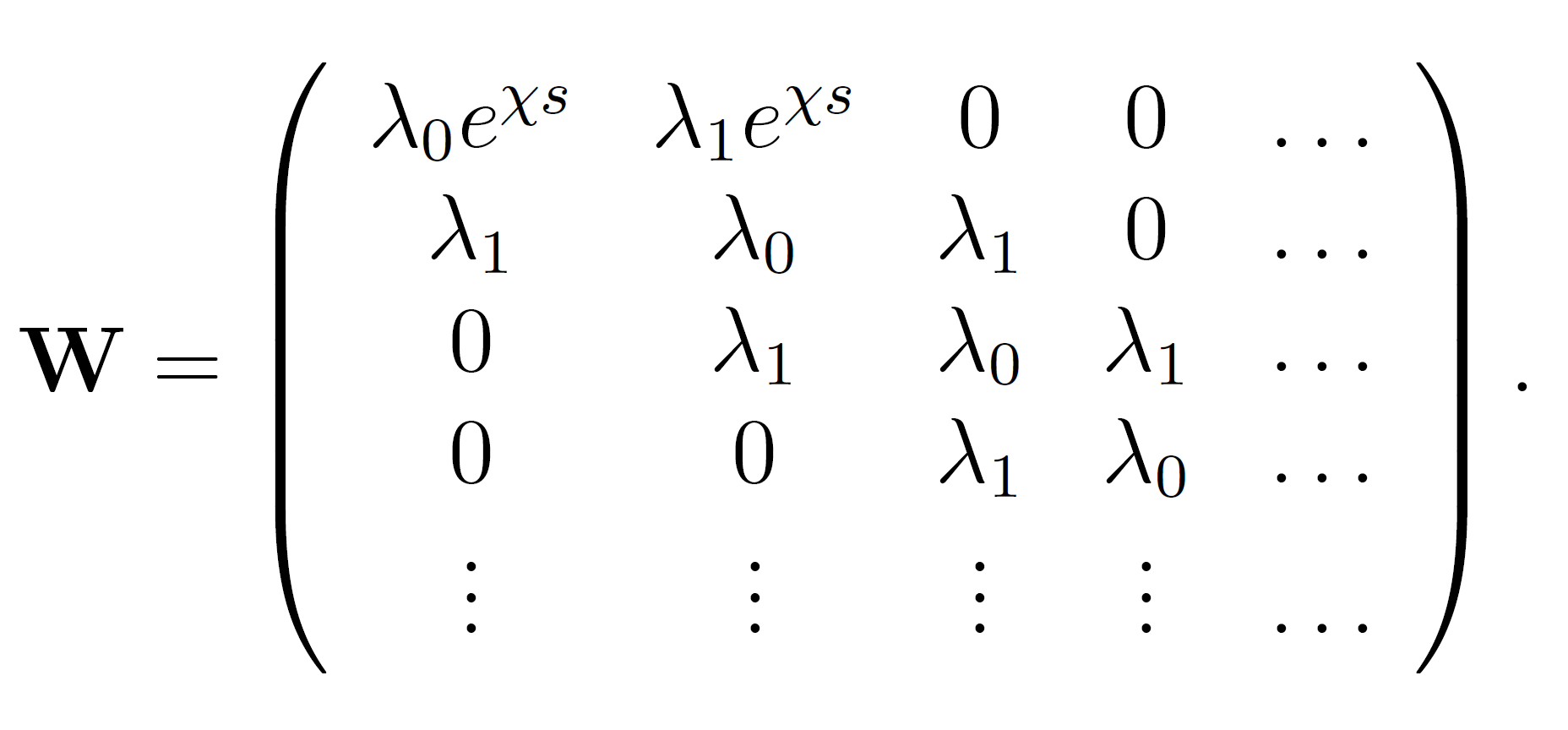
As the starting vector we choose G(0) = (eχs, 0, 0,...,0). This choice for G(0) assures that all random walks start in the surface layer. This can be easily verified. For example, two iterations result in
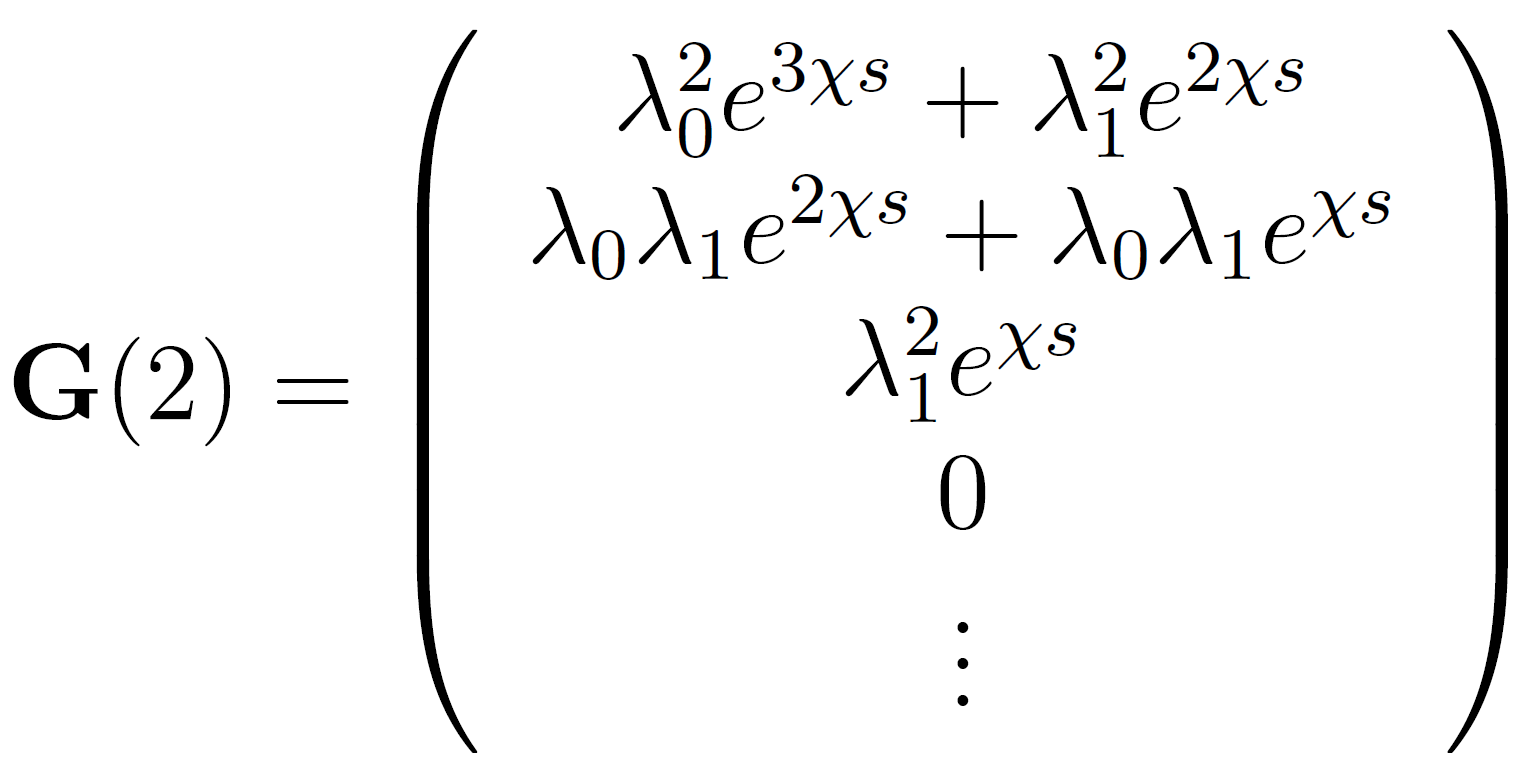
In this matrix, each polymer conformation is weighted by the proper Boltzmann factor. For example, for three segments (two bonds) with the first and last unit in the surface layer, the unnormalized probability reads
![]()
The first term is the probability that all
three units (connected by 2 bonds) lie in the surface layer, whereas
the second term is the probability that only the first and third
unit touch the surface.
As will be shown in part 2, the
conformational partition function
QN+1 along with various statistical properties can be directly calculated from the relative probabilities
G(0)....G(N). The matrix procedure outlined above,
however, is only applicable to lattice polymers in the melt or theta state where the
effects of monomer-solvent interaction and excluded volume can
be neglected. For all other cases, the matrix has to be
modified to incorporate both effects in each layer. This leads
to complicated expressions which have to be solved by an iterative procedure.6,7
References & Notes
- P. J. Flory, J. Chem. Phys. 9, 660 (1941); 10, 51 (1942)
- M. L. Huggins, J. Phys. Chem. 46, 151 (1942); J. Am. Chem. Soc. 64, 1712 (1942)
- E. A. DiMarzio,, J. Chem. Phys., 42, 2101 (1965)
- R. J. Rubin, J. Chem. Phys., 43, 2392 (1965)
- E. A. DiMarzio & R. J. Rubin, J. Chem. Phys., 55, 4318 (1971)
- R. J. Roe, J. Chem. Phys., 60, 4192 (1974)
- J. M. H. M. Scheutjens & G. J. Fleer, J. Phys. Chem. 83, 1620 (1979) & 84, 178 (1980)
The transition matrix formalism has also been used by Flory to calculate the conformations
of linear polymer chains using discrete rotational isomeric states.9- P. J. Flory, Statistical Mechanics of Chain Molecules, Wiley, New York (1969)
- A. Silberberg, J. Chem. Phys., 46, 1105 (1967)